Exercise 4.3

Fig. 14 Block diagram of the DC-servomotor.

In Fig. 14 the block diagram of a DC-servomotor is illustrated.

In this system, the input voltage \(u\) first goes through a isolated DC-DC convert[1], which applies the desired voltage \(u\) to the motor. This converter is modeled by the first-order transfer function with time constant \(T=10\) ms.

The voltage is then applied to the motor, described by a second order transfer function with gaim \(k_m=10\), electrical time constant \(T_2 =25\) ms, and mechanical time constant \(T_1 = 50\) ms.

The servomotor is first tested with \(F(s) = 1\), but the closed-loop turns out to be too slow.

1. Find \(F(s) = K\) so thatthe closed-loop is twice as fast as for \(F(s)=1\).

2. Then, find \(K\) so that the following accuracy requirements are sastisfied:

   • When \(\theta_{ref}(t) = \textrm{step}(t)\), at steady state \(\lvert \theta - \theta_{ref} \lvert \leq 0.001\)

   • When \(\theta_{ref}(t) = 10 \cdot \textrm{ramp}(t)\), at steady state \(\lvert \theta(t) - \theta_{ref}(t) \lvert \leq 0.01\)

3. (Extra!) Assume that the motor current can be measured. With the help of MATLAB, design a cascade control scheme for \(G_2(s) = \frac{Z(s)}{U(s)} = \frac{1}{(1+sT)(1+sT_2)}\) and \(G_1(s) = \frac{Y(s)}{Z(s)} \frac{10}{s(1+sT_1)}\), so that the phase margin is at least \(60^\circ\), and the bandwidth of the servomotr is at least \(100\) rad/s.

---

Solution

Question 1

First of all, let’s compute the bandwith for \(F(s) = K = 1\). The open loop transfer function is defined as

(7)\[ G_o(s) = F(s) G(s) = K \frac{10}{s(1+sT)(1+sT_1)(1+sT_2)} \]

while the closed-loop transfer function is

(8)\[ G_c(s) = \frac{G_o(s)}{1+G_o(s)} = \frac{10 K}{(T T_1 T_2)s^4 + (T T_1 + T T_2 + T_1 T_2) s^3 + (T+T_1+T_2 + T) s^2 + s + 10 K} \]

Finding \(\omega_B\) such that \(\lvert G_c(i \omega_B) \lvert = \frac{1}{\sqrt{2}}\) is impractical because of its high order.

Instead, we can sketch the Bode plot of \(G_o(s)\) and compute the critical frequency \(\omega_c \approx \omega_B\).

s = tf('s');
G = 10 / (s * (1 + 0.01*s) * (1 + 0.025*s) * (1 + 0.05*s));
figure;
bode(G, {1, 1000});
grid on;

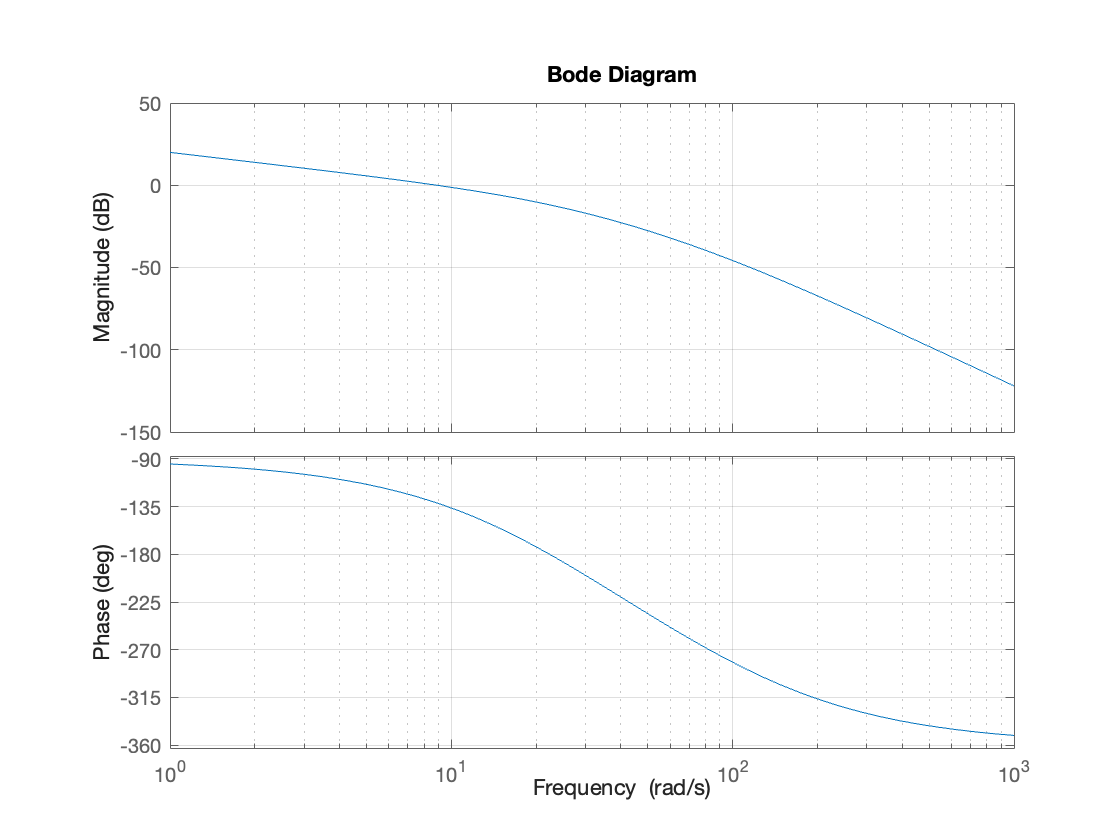
The bandwidth for \(K=1\) is approximately \(9\) rad/s.

This means we are required to find \(K\) such that the critical frequency is \(18\) rad/s. Looking at the Bode plot of \(G(s)\), we can see that \(\lvert G(i 18) \lvert_{\text{dB}} \approx -8 \) dB.

fprintf('Magnitude at 18 rad/s: %.1f dB\n', mag2db(abs(freqresp(G, 18))));

Magnitude at 18 rad/s: -8.6 dB

Therefore, taking \(K = 8.6 \text{ dB } = 2.7\) we get an open-loop transfer function with critical frequency \(\omega_c = 18\) rad/s

Go = 2.7 * G;
figure; 
bode(Go, {1, 1000});
grid on;

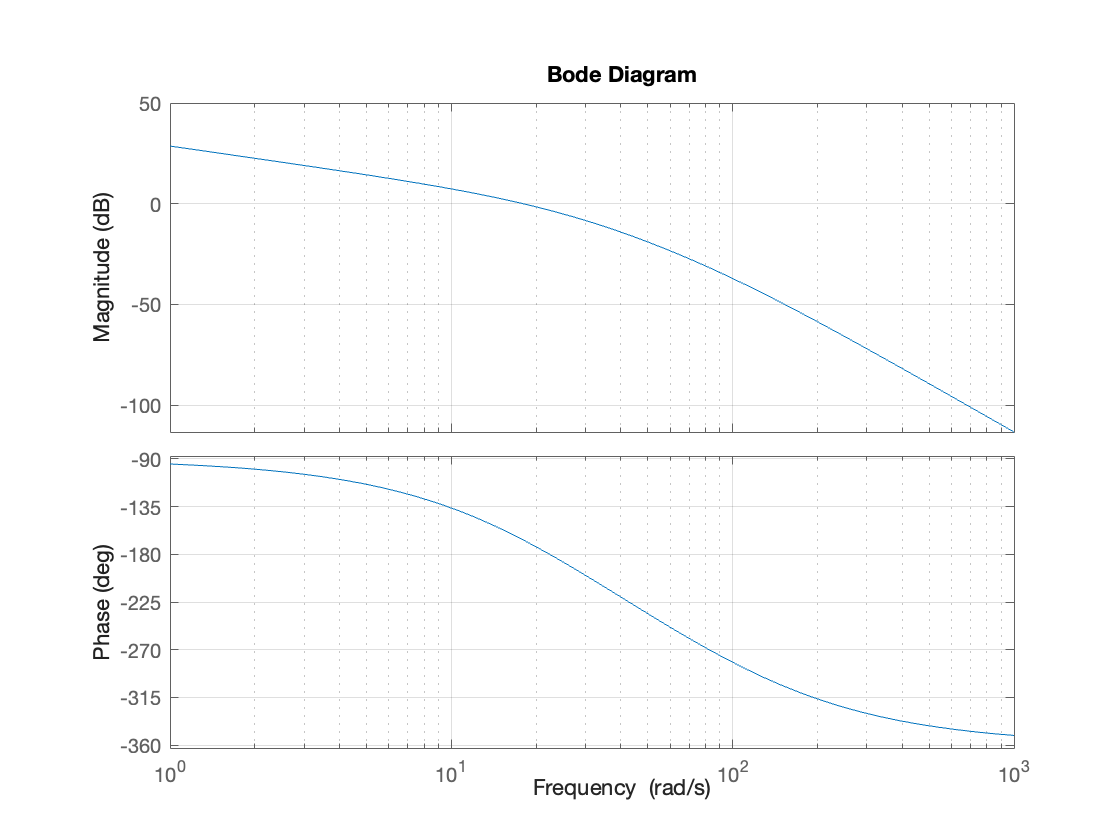
Note

Remember that \(\omega_B\) is not exactly equal to the critical frequency \(\omega_c\). It is just a useful approximation!

G_c = G / (1 + G); % Closed looop transfer function for K=1
[mag, ~, w] = bode(G_c, {1, 1000});
w_b = w(find(mag > 1/sqrt(2), 1, 'last'));
fprintf('Closed-loop bandwidth for K=1 is %.2f rad/s, while the critical frequency is %.0f rad/s\n', w_b, 9);

G_c = Go / (1 + Go); % Closed looop transfer function for K=2.7
[mag, ~, w] = bode(G_c, {1, 1000});
w_b = w(find(mag > 1/sqrt(2), 1, 'last'));
fprintf('Closed-loop bandwidth for K=2.7 is %.2f rad/s, while the critical frequency is %.0f rad/s\n', w_b, 18);

Closed-loop bandwidth for K=1 is 14.42 rad/s, while the critical frequency is 9 rad/s
Closed-loop bandwidth for K=2.7 is 28.45 rad/s, while the critical frequency is 18 rad/s

Question 2

Consider the open-loop transfer function (7) and the closed-loop transfer function (8) for a generic gain \(K\).

We start by analyzing for what values of \(K\) the closed-loop remains stable. For this, we can use root locus.

figure;
rlocus(G); hold on; % Plot the root locus

% Plot the closed-loop poles for specific values of K
K_points = [2.7, 3.9];
for k=K_points
    Gok = k * G;
    [num, den] = tfdata(Gok, "vector");
    poles = roots(num + den);
    p = plot(real(poles), imag(poles), 's', 'MarkerSize', 10, 'MarkerFaceColor', 'auto', 'DisplayName', sprintf('K=%.2f', k));
    set(p, 'markerfacecolor', get(p, 'color'));
end
legend('Location', 'northwest'); hold off;

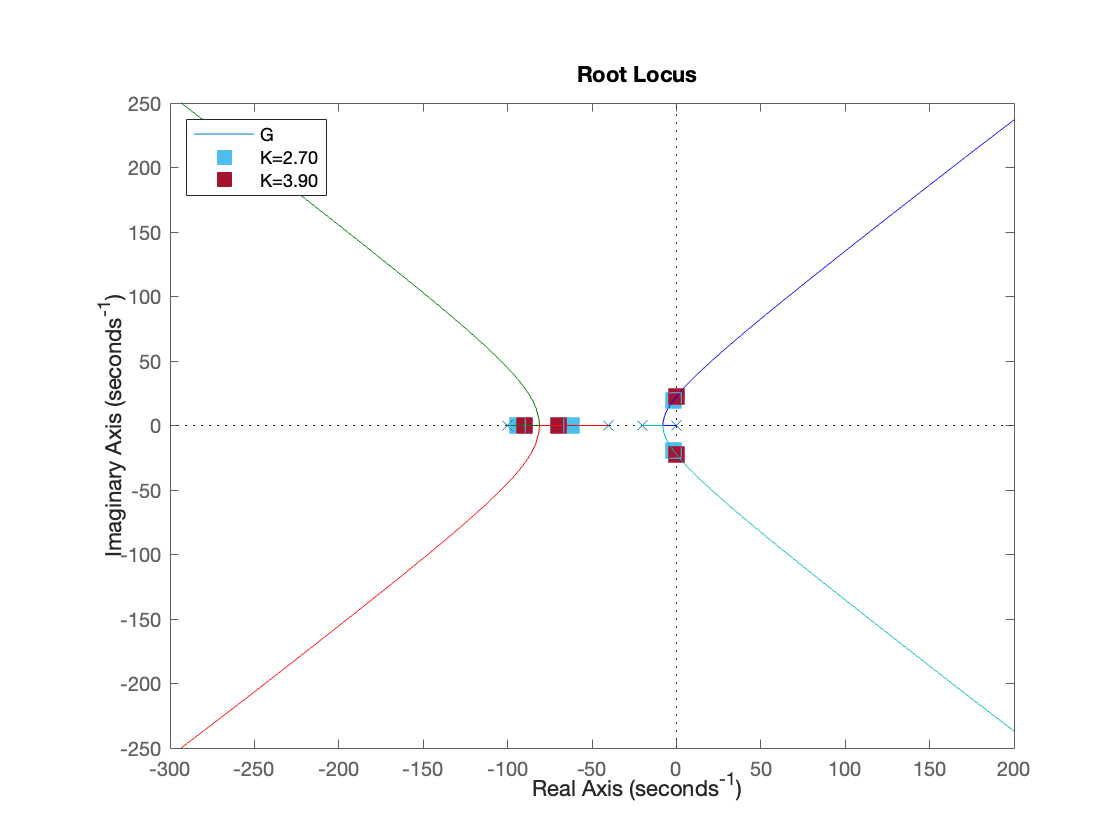
The closed-loop is stable for \(0 < K < 3.9\).

Error for step references

For step references, i.e. \(\theta_{ref}(t) = \textrm{step}(t)\), the steady-state tracking error is exactly \(0\), provided that the closed loop is stable (\(0 < K < 3.9\)). In fact, the type of \(G_o(s)\) is \(g=1\), because \(G_o(s)\) has exactly one pole in \(s=0\).

Error for ramp references

When it comes to \(\theta_{ref}(t) = 10 \cdot \textrm{ramp}(t)\), we can apply the Final Value Theorem

\[ e(t) = \lim_{s \to 0} s \big[ 1 - G_c(s)] \frac{10}{s^2} = \lim_{s \to 0} \frac{\cancel{s} + h.o.t.}{h.o.t. + 10 K} \frac{10}{\cancel{s}} = \frac{1}{K} \]

In order to get the desired \(1\%\) accuracy we would need \(K> 100\), which unfortunately breaks the closed-loop stability assumption of the Final Value Theorem!

Question 3

The solution will be provided over the next few weeks.

Hints:

• Use PD controllers for both the outer and the inner control loop.

• Use the function margin(Go) to evaluate the phase and gain margin given the open loop transfer function Go

• Remember that the bandwidth of the inner loop must be at least \(10\times\) larger than that of the outer loop.

[1]

A DC-DC isolated converter is an electronic device that applies the desired control signal \(u\) to the motor while keeping the controller board electrically insulated from the high-current/high-voltage motor circuit.