Exercise 2.3

Fig. 7 Closed-loop system

Depicted above is the block diagram of a closed-loop system.

1. For what values of the controller parameter \(K\) is the closed-loop stable?

2. Is there any value of \(K\) such that the closed-loop can track the reference signal \(r(t) = 0.1 \textrm{ramp}(t)\) with an error less than \(5 \cdot 10^{-3}\)?

---

Solution

Question 1

The open-loop transfer function of the system is

\[ G_o(s) = K \frac{1}{s(s+1)(s+2)} \]

The closed-loop transfer function is

\[ G_c(s) = \frac{G_o(s)}{1 + G_o(s)} = \frac{K}{s^3 + 3s^2 + 2s + K} \]

Unfortunately, \(G_c(s)\) is a third-order transfer function, therefore we cannot analytically inspect how the poles of \(G_c(s)\) change as a function of \(K\).

Two approaches can be used to solve the exercise:

• Using the Routh stability criterion

• Using the rootlocus

Because the former is out of the scope of this course, we will go for the second one. Let’s plot the root locus of \(G_o(s)\)

s = tf('s');
Go = 1/(s*(s+1)*(s+2));

rlocus(Go); hold on; % Plot the root locus

% Plot the closed-loop poles for specific values of K
K_points = [0.4, 6, 20];
for k=K_points
    Gok = k * Go;
    [num, den] = tfdata(Gok, "vector");
    poles = roots(num + den);
    p = plot(real(poles), imag(poles), 's', 'MarkerSize', 10, 'MarkerFaceColor', 'auto', 'DisplayName', sprintf('K=%.2f', k));
    set(p, 'markerfacecolor', get(p, 'color'));
end
legend('Location', 'northwest'); hold off;

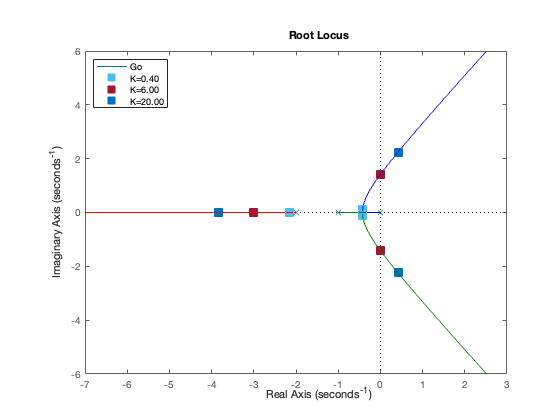
Note that:

• For \(0 < K \leq 0.4\), the closed-loop are real-valued and negative

• For \(0.4 < K < 6\) we have 1 real-valued negative pole and two complex-conjugate (dominating) poles with negative real part.

• For \(K >6\) the two complex-conjugate poles have positive real part, so the closed-loop is unstable.

The solution is therefore \(0 < K < 6\).

Question 2

Under the assumption that the closed-loop is stable (\(0 < K < 6\)), we can apply the Final Value Theorem, where the reference is \(R(s) = \frac{0.1}{s^2}\).

Recalling that Laplace transform of the error is \(E(s) = R(s) - Y(s) = (1 - G_c(s)) R(s)\),

\[\begin{split} \begin{aligned} \lim_{t \to \infty} e(t) = \lim_{s \to 0} s \left[ 1 - G_c(s) \right] \frac{0.1}{s^2} &= \lim_{s \to 0} s \frac{s^3 + 3 s^2 + 2s }{s^3 + 3 s^2 + 2s + K} \frac{0.1}{s^2} \\ &= \lim_{s \to 0} \frac{s^2 + 3 s + 2 }{s^3 + 3 s^2 + 2s + K} 0.1 = \frac{0.2}{K} \end{aligned} \end{split}\]

To get the desired error, we impose

\[ \frac{0.2}{K} \leq 0.005 \quad \implies \quad K \geq 40 \]

Unfortunately, this error is not achievable because for \(K > 6\) the closed-loop is unstable.