Exercise 1.4#
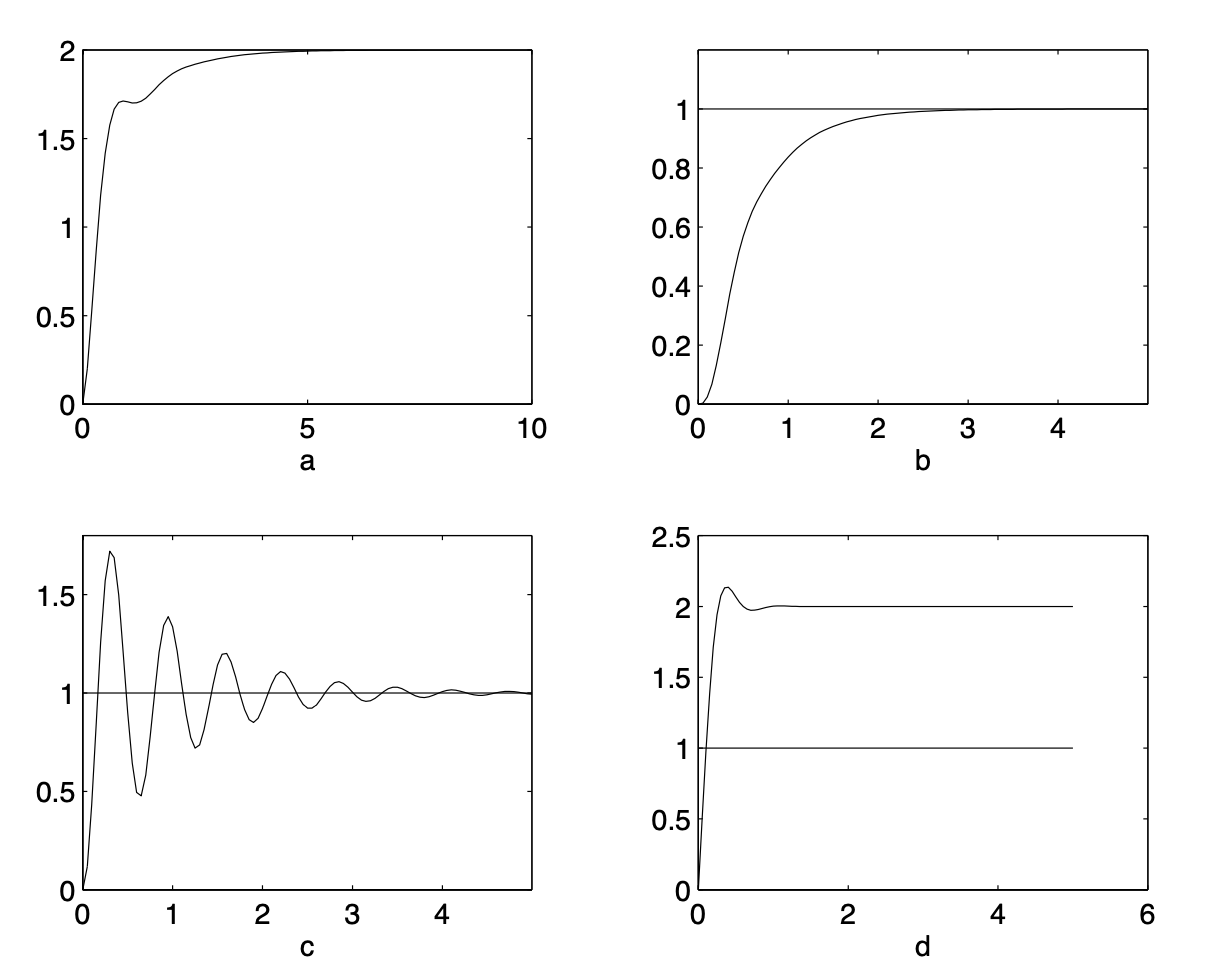
Fig. 3 Step responses to consider (courtesy of Exercise Manual for Automatic Control)#
Pair each step response in the plot above with the correct transfer function from the list below:
\(G_1(s) = \frac{100}{s^2 + 2s + 100}\)
\(G_2(s) = \frac{1}{s+2}\)
\(G_3(s) = \frac{10 s^2 + 200s + 2000}{(s+10)(s^2 + 10s + 100)}\)
\(G_4(s) = \frac{100}{s^2 + 10s + 100} \cdot \frac{2}{s+2}\)
\(G_5(s) = \frac{100}{s^2 + 10s + 100} + \frac{2}{s+2}\)
\(G_6(s) = \frac{100}{s^2 - 10s + 100} \cdot \frac{1}{s+2}\)
Solution#
Considering a stable transfer function \(G(s)\), the following facts can be considered.
If \(G(s)\) has order greater than two, the dominant poles are those with the smallest (least negative) real part.
The empirical rule for estimating the 99% settling time \(T_{99\%}\) of \(G(s)\) is \(T_{99\%} \approx \frac{4.6}{-\alpha_d}\), where \(\alpha_d\) is the real part of the dominant pole.
If the dominant poles are complex conjugate, the step response is oscillatory. Letting \(\alpha\) and \(\beta\) be the real and imaginary parts of the complex eigenvalues, respectively, the damping coefficient \(\xi\) is defined as \(\xi = \frac{-\alpha}{\sqrt{\alpha^2 + \beta^2}}\).
Overdamped systems: \(\xi \sim 0.75 \div 1.0\)
Damped systems: \(\xi \sim 0.5 \div 0.75\)
Underdamped systems: \(\xi \sim 0 \div 0.5\)
The steady-state output is \(y(\infty) = G(0) u(\infty)\).
\(G_1(s)\)#
Second order transfer function
Unitary static gain – \(G_1(0) = 1\)
Underdamped (highly oscillatory)
\(T_{99\%} \approx 4.6\) seconds
These characteristics match plot (c)
\(G_2(s)\)#
First order transfer function
Static gain \(G_2(0) = 0.5\)
\(T_{99\%} \approx 2.3\) seconds
\(G_3(s)\)#
Dominant poles: complex-conjugate eigenvalues
Static gain \(G_3(0) = 2\)
\(T_{99\%} \approx 0.9\) seconds
These characteristics match plot (d)
\(G_4(s)\)#
Dominant pole: real pole in \(-2\)
Unitary static gain \(G_4(0) = 1\)
\(T_{99\%} \approx 2.3\) seconds
These characteristics match plot (b)
\(G_5(s)\)#
Dominant pole: real pole in \(-2\)
Static gain \(G_5(0) = 2\)
\(T_{99\%} \approx 2.3\) seconds
These characteristics match plot (a)
\(G_6(s)\)#
Unstable eigenvalues!
