Exercise 1.2#
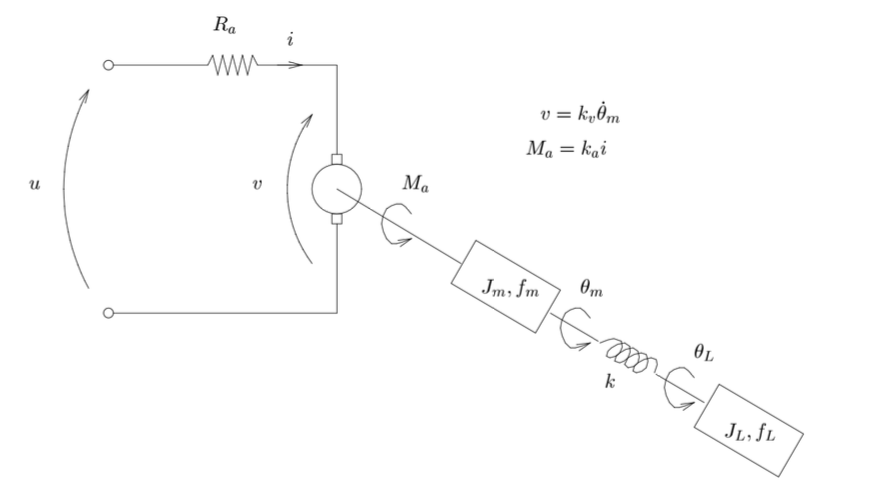
Fig. 2 Schematic of the motor with a load (courtesy of Exercise Manual for Automatic Control)#
Assume that the DC-motor in Exercise 1.1 is running a load attached to an elastic axis, as in the figure above. Let \(k\) be the axis’ spring constant, and let \(J_L\) be the moment of inertia of the load.
Write the transfer function between the input voltage \(u\) and the angle \(\theta_L\).
Solution#
Writing the momentum balance of the load and of the motor we get, respectively
\[\begin{split}
\begin{aligned}
J_L \ddot{\theta}_L =& - f_L \dot{\theta}_L - k (\theta_L - \theta_m) \\
J_m \ddot{\theta}_m =& -f_m \dot{\theta}_m + k (\theta_L - \theta_m) + k_a i
\end{aligned}
\end{split}\]
Moving to the Laplace domain,
\[\begin{split}
\begin{aligned}
J_L s^2 {\Theta}_L(s) =& - f_L s {\Theta}_L(s) - k (\Theta_L(s) - \Theta_m(s)) \\
J_m s^2 {\Theta}_m(s) =& -f_m s {\Theta}_m(s) + k (\Theta_L(s) - \Theta_m(s)) + k_a I(s)
\end{aligned}
\end{split}\]
We can isolate \(\Theta_m(s)\) from the second equation:
\[
\Theta_m(s) = \frac{k}{J_m s^2 + f_m s + k} \Theta_L(s) + \frac{k_a}{J_m s^2+ f_m s + k} I(s)
\]
Replacing it back into the first equation, we get
\[
(J_L s^2 + f_L s + k) \Theta_L(s) = \frac{k^2}{J_m s^2 + f_m s + k} \Theta_L(s) + \frac{k \cdot k_a}{J_m s^2+ f_m s + k} I(s)
\]
Isolating \(\Theta_L(s)\), and recalling that \(I(s) = \frac{U(s)}{R_a}\), we finally get our transfer function
\[
\Theta_L(s) = \frac{\frac{k \cdot k_a}{R_a}}{J_m J_L s^4 + (J_m f_L + J_L f_m)s^3 + (k J_m + k J_L + f_M f_L) s^2 + k(f_L + f_m) s} U(s)
\]
