Exercise 3.4

Exercise 3.4#

../_images/ex4.svg

Fig. 8 Block diagram of the closed loop#

A system \(G(s)\) is controlled using a feedback with a proportional controller according to Fig. 8. \(G(s)\) has no unstable pole, that is, no pole with positive real part.

In Fig. 9, the Nyquist diagram of four different systems \(G(s)\) are reported. Find, for each of these systems, the values of \(K\) for which the closed-loop is stable.

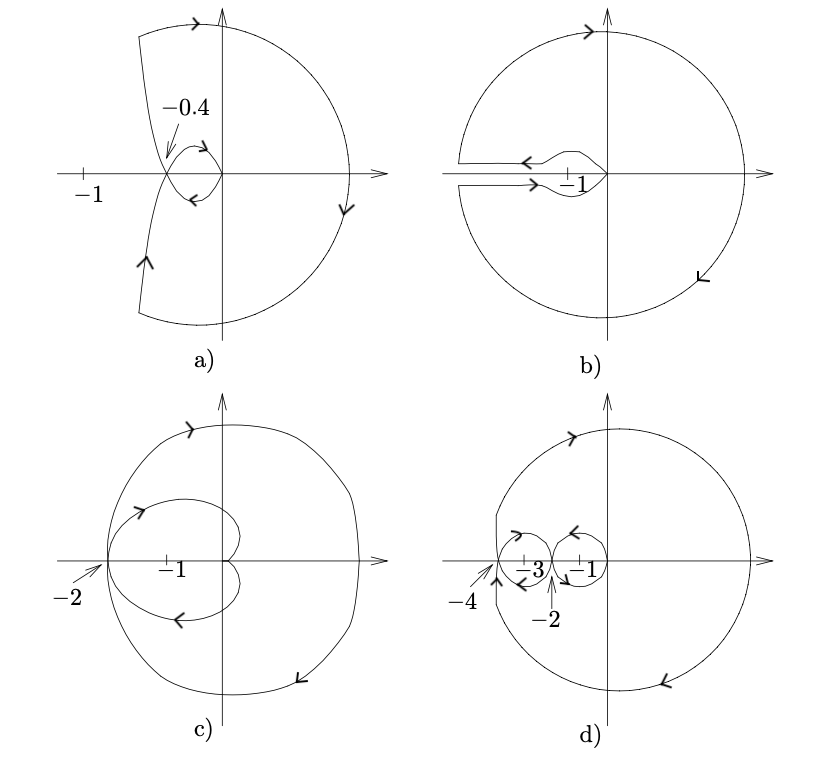
../_images/ex4-nyq.png

Fig. 9 Nyquist plots of \(G(s)\)#

Solution#

The Nyquist criterion allows to assess the closed-loop stability, that is, the stability of the closed-loop transfer function \(G_c(s) = \frac{F(s)G(s)}{1 + F(s)G(s)}\) by analyzing the Nyquist plot of the open-loop transfer function \(G_o(s) = F(s)G(s)\).

Let’s refresh the Nyquist theorem in the case where \(G_o(s)\) does not have unstable poles.

Nyquist criterion

The closed-loop \(G_c(s)\) is stable if and only if the Nyquist plot enrircles the point \(-1\) the same number of times in both clockwise and counterclockwise directions.

Note that the case where the Nyquist plot passes through the point \(-1\) is not well defined.

Plot (a)#

We start by pointing out that the Nyquist criterion is satisfied for \(K=1\), since \(N_{cw} = N_{ccw} = 0\), where \(N_{cw}\) and \(N_{ccw}\) are the number of clockwise and counter-clockwise encirclements of \(-1\).

Because the effect of \(K\) is to scale up/down the Nyquist plot of \(G_o(s)\), the Nyquist criterion is satisfied for any \(0 < K < 2.5\). In fact, when \(K = 2.5\), the point \(-0.4\) overlaps with \(-1\)!

\(K > 2.5\) leads to instability since \(N_{cw} = 2\) while \(N_{ccw} = 0\).

Plot (b)#

Since the Nyquist plot is not intersecting the real negative semi-axis, there exists no \(K\) for which the point \(-1\) is encircled.

Therefore the Nyquist criterion is satisfied \(\forall K\).

Plot (c)#

For \(K=1\), the Nyquist plot does not satisfy the Nyquist criterion, since \(N_{cw}=2\) and \(N_{ccw}=0\).

However, picking \(0 < K < 0.5\), the Nyquist criterion is satisfied since \(-1\) is not enricled (the intersection with the real negative semi-axis becomes \(-2K > -1\)).

Plot (d)#

We start by noting that the Nyquist plot of \(G_o(s) = K G(s)\) intersects the real negative semi-axis in \(-4K\) and \(-2K\).

Therefore

  • For \(0 < K < 0.25\), the Nyquist criterion is satisfied because the plot does not encircle \(-1\).

  • For \(0 < K < 0.5\), the Nyquist criterion is not satisfied because \(N_{cw} = 2\) and \(N_{ccw} = 0\).

  • For \(K > 0.5\), the Nyquist criterion is satisfied because \(N_{cw} = N_{ccw} = 1\).

Solution: \(0 < K < 0.25 \cup K > 0.5\).