Exercise 1.3

Exercise 1.3#

Assume that the DC motor described in Exercise 1.2 is controlled by a Proportional (P) controller.

  1. Sketch the block diagram of the control system. Determine how the poles of the closed-loop depend on the proportional gain \(K\), and discuss what this means for the behavior of the closed-loop.

  2. Consider two reference signals, a step \(\theta_{ref}(t) = \textrm{step}(t)\) and a ramp \(\theta_{ref}(t) = \textrm{ramp}(t)\). What is the steady-state controll error (or output tracking error) in these two cases?

  3. Consider now a Proportional Integral (PI) controller. What will the steady-state error be if the reference signal is a ramp?

Solution#

As shown in Exercise 1.1, the transfer function of the motor is

\[ G(s) = \frac{k_o}{s(s+\alpha)} \]

The open-loop transfer function is defined as

\[ G_o(s) = \frac{\Theta(s)}{\Theta_{ref}(s)} = F(s) \cdot G(s) \]

where \(\Theta_{ref}(s)\) is the reference signal, and \(F(s)\) is the controller.

We now compute the closed-loop transfer function as

\[ \Theta(s) = G(s) F(s) \underbrace{(\Theta_{ref}(s) - \Theta(s))}_{\text{Error $E(s)$}} \quad \Rightarrow \quad \Theta(s) = \frac{F(s)G(s)}{1 + F(s) G(s)} \Theta_{ref}(s) = \frac{G_o(s)}{1+G_o(s)} \Theta_{ref}(s) \]

Question 1#

We start by considering a proportional controller, \(F(s) = K\), where \(K\) is the proportional gain.

In this case, the closed loop transfer function is

\[ G_{c}(s) = \frac{K \cdot \frac{k_o}{s(s+\alpha)}}{1+K \cdot \frac{k_o}{s(s+\alpha)}} = \frac{k_o K}{s^2 + \alpha s +k_o K} \]

The closed-loop poles are the poles of \(G_c(s)\). We hence need to find the roots of the denominator of \(G_c(s)\):

\[ s^2 + \alpha s + k_o K = 0 \]

We solve this equation by \(s\). The discriminant is \(\Delta = {\alpha^2 - 4 k_o K}\).

Now, there are two relevant cases.

Case \(\Delta \geq 0\)#

When \(K < \frac{\alpha^2}{4 k_o}\) the discriminant is positive, which means that there exist two real poles:

\[ s = \frac{-\alpha \pm \sqrt{\Delta}}{2} \]

These poles are stable as long as both of them are strictly negative.

  • \(- \alpha - \sqrt{\Delta} < 0 \quad \rightarrow \quad \sqrt{\Delta} > -\alpha\)

  • \(- \alpha + \sqrt{\Delta} < 0 \quad \rightarrow \quad \sqrt{\Delta} < \alpha\)

The first is always satisfied as long as \(\Delta \geq 0\). When it comes to the second one, under the condition \(\Delta \geq 0\) we can square both sides since \(\alpha > 0\).

This way, we get the following system of inequalities

\[\begin{split} \begin{dcases} K \leq \frac{\alpha^2}{4 k_o} \\ \alpha^2 - 4 k_o K < \alpha^2 \end{dcases} \,\, \Rightarrow \,\, \begin{dcases} K \leq \frac{\alpha^2}{4 k_o} \\ K > 0 \end{dcases} \,\, \Rightarrow \,\, 0 < K \leq \frac{\alpha^2}{4 k_o} \end{split}\]

Case \(\Delta < 0\)#

When \(K > \frac{\alpha^2}{4 k_o}\) the discriminant is negative, which means that we have two complex conjugate poles.

In this case, it is easy to notice that

\[ s = -\frac{\alpha}{2} \pm i \frac{\sqrt{\lvert \Delta \lvert}}{2} \]

In this case the real part of these eigenvalues is \(-\frac{\alpha}{2} < 0\) regardless of \(K\). Therefore, any \(K > \frac{\alpha^2}{4 k_o}\) makes the closed-loop stable.

Solution to Question 1#

The overall solution is given by the union of the solutions in the two cases:

\[ \left\{ K \geq \frac{\alpha^2}{4 k_o} \cup K < \frac{\alpha^2}{4 k_o} \right\} = {K > 0} \]

Note

An alternative (and faster) approach to solve the problem would be to use the so-called Routh criterion!

Finally, we can visualize how the closed-loop poles move in the complex plane as a function of \(K\) by inspecting the root locus. We will plot the root locus with MATLAB assuming \(k_o = 1\) and \(\alpha=1\).

s = tf('s');
G = 1/(s*(s+1));

rlocus(G); hold on; % Plot the root locus

% Plot the closed-loop poles for specific values of K
K_points = [0.2, 0.3];
for k=K_points
    Go = k * G;
    [num, den] = tfdata(Go, "vector");
    poles = roots(num + den);
    p = plot(real(poles), imag(poles), 's', 'MarkerSize', 10, 'MarkerFaceColor', 'auto', 'DisplayName', sprintf('K=%.2f', k));
    set(p, 'markerfacecolor', get(p, 'color'));
end
legend('Location', 'northwest'); hold off;
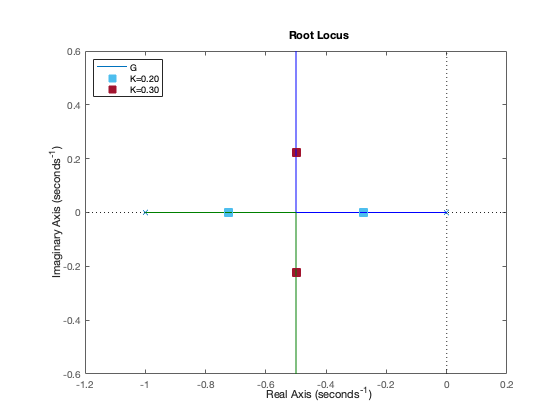
../_images/af2f632bd587391b4ea4a910bfc511005edb08d3b017138119994a7cc1e46823.png

As one can see from the plot above, for every \(K > 0\) the closed-loop eigenvalues have negative real part.

Warning

Interactive root locus plots are unfortunately not supported. To get the closed-loop poles for specific values of \(K\) you can

  • Run this notebook in Binder and add put the value of interest in K_points.

  • Run rlocus(G) in MATLAB, which will create an interactive point.

  • Run rlocusx(G) in a GUI installation of Octave.

Question 2#

Recalling that \(\Theta(s) = G_c(s) \Theta_{ref}(s)\), where \(G_c(s)\) is the closed-loop transfer function, since we have verified that \(G_c(s) = \frac{k_o K}{s^2 + \alpha s + k_o K}\) is stable for any \(K > 0\), we can apply the Final Value Theorem.

According to the Final Value Theorem,

\[ \lim_{t \to \infty} \theta(t) = \lim_{s \to 0} s G_c(s) \Theta_{ref}(s) \]

From this, the final error is

\[ \lim_{t \to \infty} e(t) = \lim_{t \to \infty} \theta_{ref}(t) - \lim_{t \to \infty} \theta(t) = \lim_{s \to 0} s\left[ 1 - G_c(s) \right] \Theta_{ref}(s) \]

Case \(\theta_{ref}(t) = \textrm{step}(t)\)#

\[ e(\infty) = \lim_{s\to 0} \cancel{s} \left[ 1 - \frac{k_o K}{s^2 + \alpha s + k_o K} \right] \frac{1}{\cancel{s}} = \lim_{s\to 0} \frac{s^2 + \alpha s}{s^2 + \alpha s + k_o K} = 0 \]

Case \(\theta_{ref}(t) = \textrm{ramp}(t)\)#

\[ e(\infty) = \lim_{s\to 0} \cancel{s} \left[ 1 - \frac{k_o K}{s^2 + \alpha s + k_o K} \right] \frac{1}{s^{\cancel{2}}} = \lim_{s\to 0} \frac{s^2 + \alpha s}{s^2 + \alpha s + k_o K} \frac{1}{s} = \frac{\alpha}{k_o K} \neq 0 \]

Question 3#

We now consider the case where we have a PI controller:

\[ F(s) = \frac{k_i}{s} + k_p = \frac{k_p s + k_i}{s} \]

where \(k_p\) is the proportional gain and \(k_i\) is the integral gain. The closed-loop transfer function becomes

\[\begin{split} \begin{aligned} G_c(s) =& \frac{F(s) G(s)}{1 + F(s) G(s)} \\ =& \frac{(k_p s + k_i) k_o}{s^2(s+\alpha) + k_o (k_p s + k_i)}\\ =& \frac{(k_p s + k_i) k_o}{s^3 + \alpha s^2 + k_o k_p s + k_o k_i} \end{aligned} \end{split}\]

Assuming that \(G_c(s)\) is stable, i.e. \(k_p\) and \(k_i\) are designed so that all the roots of \(s^3 + \alpha s^2 + k_o k_p s + k_o k_i = 0\) have negative real part[1], then we can apply the Final Value theorem.

\[ e(\infty) = \lim_{s \to 0} s \left[ 1 - \frac{(k_p s + k_i) k_o}{s^3 + \alpha s^2 + k_o k_p s + k_o k_i} \right] \frac{1}{s^2} = \lim_{s \to 0} \frac{s^3 + \alpha s^2}{s^3 + \alpha s^2 + k_o k_p s + k_o k_i} \frac{1}{s} = 0 \]